

緊接著要介紹議題是分類,本次文章將會帶您深入了解分類的相關內容,一起看下去吧
正如之前課程提過,分類模型可以將輸入資料判定為某一特定類別或群組的成員。在實務應用中,羅吉斯迴歸 (Logistic Regression) 是一種常見的分類模型。羅吉斯迴歸以 Logistic 函數(也稱為 Sigmoid 函數)這個作為其核心的數學函數作為命名。這個函數在 19 世紀中期被提出,用於類比一個地區人口的指數成長,同時考慮到環境的承載能力。環境承載能力指的是在可用的資源和服務條件下,一個生態系統可以無限期支援的最大人口規模。例如,可以在一艘救生艇上存活的人數取決於有多少食物與飲用水、每個人每天需要多少食物與飲用水來維持生命、以及平均在救生艇上呆多少天才有可能獲救等因素。羅吉斯迴歸透過估算機率的方式來衡量一個分類型的應變數與一個或多個自變數之間的關係。
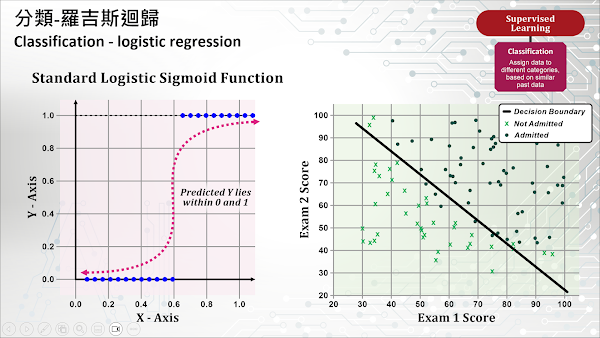
Logistic 函數產生一個 S 型曲線,將任何實數映射到一個 0 與 1 之間的數值,這個數值代表某個物件屬於某個特定群組或分類的機率。您可以將羅吉斯迴歸想像成一種“On-Off 開關”,輸入資料在一開始的一段時間被解釋為“關閉(0)”狀態,但從某個時刻開始會被切換為“開啟(1)”狀態並保持不變。一個臨界值 (Threshold) 被用來指示這個開關在什麼值上從“關閉”狀態切換到“開啟”狀態。通常,這個數值為 0.5,如果 Logistic 函數的輸出大於 0.5,結果會被歸類為 1(或 True),反之,則歸類為 0(或 False)。如果這個機率分數接近 1,意味著觀測值非常可能屬於某個特定群組或分類。
舉一個簡單的例子,假設我們使用羅吉斯迴歸模型來預測一個學生是否有機會被一所著名大學錄取。如果該模型只考慮兩次入學考試的分數,並推斷出 0.932 的數值,這意味著該名學生有 93.2% 的概率會被錄取(假設允許入學的學生數量沒有上限,且使用的臨界值是 0.5)。更確切地說,模型預測為 0.932 的一組學生在 93.2% 的情況下會被錄取,而在 6.8% 的情況下不會被錄取。上圖右側的圖例以一個極簡化的方式協助您理解羅吉斯迴歸模型的分類結果,該斜線右上方的點代表被模型歸類於可能被錄取學生的兩次入學考試分數。由於羅吉斯迴歸模型的分類結果代表機率值,因此斜線右上方的點大部分均為被錄取的點(藍色實心圓點),但也包含了少數未被錄取的點(綠色 X 符號)。
羅吉斯迴歸屬於一種線性演算法 (Linear Algorithm),非常適合用於簡單的二元分類問題。這種演算法所建立的模型非常容易實作,訓練模型時不需要對輸入的特徵變數進行縮放,也不太需要進行變數的優化,因此不需要大量的運算資源。如果訓練資料集已經完成了維度縮減,也就是與應變數(目標變數)無關聯或是彼此間具高度關聯性的自變數(特徵變數)均已被移除,羅吉斯迴歸模型的預測效果將會更好。正因為它具備很強的可解釋性,並且可以產生較準確的預測機率,在實務中常被拿來作為解決二元分類問題時使用的模型。
羅吉斯迴歸模型有一些限制,其中之一是它無法處理非線性問題 (Non-linear problems),並且它的輸出只能預測分類的結果 (Categorical outcome)。此外,由於羅吉斯迴歸模型容易發生過度擬合 (Overfitting) 的問題,因此它已不再是最強大的分類演算法之一。在現今的機器學習領域,其他非線性分類器,如決策樹 (Decision Trees)、隨機森林 (Random Forests)、支援向量機 (Support Vector Machines, SVMs) 和神經網路 (Neural Networks) 等演算法,均已經超越了羅吉斯迴歸模型。